nyquist stability criterion calculator

that appear within the contour, that is, within the open right half plane (ORHP). , which is the contour ( ) ( Draw the Nyquist plot with \(k = 1\). There is a real estate problem: you can't show everything. 1This transfer function was concocted for the purpose of demonstration. The Nyquist criterion gives a graphical method for checking the stability of the closed loop system. ) ( (

j ( This case can be analyzed using our techniques. The frequency-response curve leading into that loop crosses the \(\operatorname{Re}[O L F R F]\) axis at about \(-0.315+j 0\); if we were to use this phase crossover to calculate gain margin, then we would find \(\mathrm{GM} \approx 1 / 0.315=3.175=10.0\) dB. The fundamental stability criterion is that the magnitude of the loop gain must be less than unity at f180. has exactly the same poles as \nonumber\]. =

In Cartesian coordinates, the real part of the transfer function is plotted on the X-axis while the imaginary part is plotted on the Y-axis. You have already encountered linear time invariant systems in 18.03 (or its equivalent) when you solved constant coefficient linear differential equations. D

In particular, there are two quantities, the gain margin and the phase margin, that can be used to quantify the stability of a system. This has one pole at \(s = 1/3\), so the closed loop system is unstable. 1 Nyquist stability criterion like N = Z P simply says that. 0 Alternatively, and more importantly, if You can achieve greater accuracy using it. be the number of poles of k You can also check that it is traversed clockwise.

{\displaystyle G(s)} Another aspect of the difference between the plots on the two figures is particularly significant: whereas the plots on Figure \(\PageIndex{1}\) cross the negative \(\operatorname{Re}[O L F R F]\) axis only once as driving frequency \(\omega\) increases, those on Figure \(\PageIndex{4}\) have two phase crossovers, i.e., the phase angle is 180 for two different values of \(\omega\). We can show this formally using Laurent series. 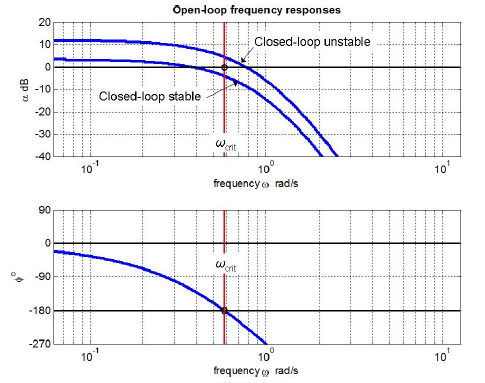BODE AND NYQUIST PLOTS Which, if either, of the values calculated from that reading, \(\mathrm{GM}=(1 / \mathrm{GM})^{-1}\) is a legitimate metric of closed-loop stability? j document.getElementById( "ak_js_1" ).setAttribute( "value", ( new Date() ).getTime() ); The system or transfer function determines the frequency response of a system, which can be visualized using Bode Plots and Nyquist Plots. WebThe Nyquist stability criterion is widely used in electronics and control system engineering, as well as other fields, for designing and analyzing systems with feedback. ) entire right half plane. \(\text{QED}\), The Nyquist criterion is a visual method which requires some way of producing the Nyquist plot. s ) 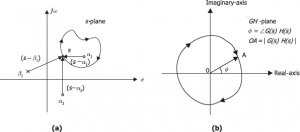Take \(G(s)\) from the previous example. G {\displaystyle G(s)} ) The system or transfer function determines the frequency response of a system, which can be visualized using Bode Plots and Nyquist Plots. Rearranging, we have \(G\) has one pole in the right half plane. in the right-half complex plane minus the number of poles of s These are the same systems as in the examples just above. Conclusions can also be reached by examining the open loop transfer function (OLTF) are also said to be the roots of the characteristic equation While Nyquist is one of the most general stability tests, it is still restricted to linear, time-invariant (LTI) systems. {\displaystyle D(s)} Answer: The closed loop system is stable for \(k\) (roughly) between 0.7 and 3.10. 0.375=3/2 (the current gain (4) multiplied by the gain margin The portion of the Nyquist plot for gain \(\Lambda=4.75\) that is closest to the negative \(\operatorname{Re}[O L F R F]\) axis is shown on Figure \(\PageIndex{5}\). ; when placed in a closed loop with negative feedback The negative phase margin indicates, to the contrary, instability. Das Stabilittskriterium von Strecker-Nyquist", "Inventing the 'black box': mathematics as a neglected enabling technology in the history of communications engineering", EIS Spectrum Analyser - a freeware program for analysis and simulation of impedance spectra, Mathematica function for creating the Nyquist plot, https://en.wikipedia.org/w/index.php?title=Nyquist_stability_criterion&oldid=1143993121, Short description is different from Wikidata, Creative Commons Attribution-ShareAlike License 3.0, However, if the graph happens to pass through the point, This page was last edited on 11 March 2023, at 05:22. {\displaystyle D(s)=1+kG(s)} ( s F s Got a suggestion: Can you also add the system gain parameter? F G ( s ( *(26- w.^2+2*j*w)); >> plot(real(olfrf007),imag(olfrf007)),grid, >> hold,plot(cos(cirangrad),sin(cirangrad)). Note that we count encirclements in the This is distinctly different from the Nyquist plots of a more common open-loop system on Figure \(\PageIndex{1}\), which approach the origin from above as frequency becomes very high. It is informative and it will turn out to be even more general to extract the same stability margins from Nyquist plots of frequency response. \(G(s)\) has one pole at \(s = -a\). u . {\displaystyle {\mathcal {T}}(s)} -plane, Notice that when the yellow dot is at either end of the axis its image on the Nyquist plot is close to 0. {\displaystyle 0+j(\omega +r)} G has zeros outside the open left-half-plane (commonly initialized as OLHP). Give zero-pole diagrams for each of the systems, \[G_1(s) = \dfrac{s}{(s + 2) (s^2 + 4s + 5)}, \ \ \ G_1(s) = \dfrac{s}{(s^2 - 4) (s^2 + 4s + 5)}, \ \ \ G_1(s) = \dfrac{s}{(s + 2) (s^2 + 4)}\]. This kind of things really helps students like me. ( D It is certainly reasonable to call a system that does this in response to a zero signal (often called no input) unstable. As \(k\) goes to 0, the Nyquist plot shrinks to a single point at the origin. For our purposes it would require and an indented contour along the imaginary axis. WebFor a given sampling rate (samples per second), the Nyquist frequency (cycles per second), is the frequency whose cycle-length (or period) is twice the interval between samples, thus 0.5 cycle/sample. The other phase crossover, at \(-4.9254+j 0\) (beyond the range of Figure \(\PageIndex{5}\)), might be the appropriate point for calculation of gain margin, since it at least indicates instability, \(\mathrm{GM}_{4.75}=1 / 4.9254=0.20303=-13.85\) dB. A With a little imagination, we infer from the Nyquist plots of Figure \(\PageIndex{1}\) that the open-loop system represented in that figure has \(\mathrm{GM}>0\) and \(\mathrm{PM}>0\) for \(0<\Lambda<\Lambda_{\mathrm{ns}}\), and that \(\mathrm{GM}>0\) and \(\mathrm{PM}>0\) for all values of gain \(\Lambda\) greater than \(\Lambda_{\mathrm{ns}}\); accordingly, the associated closed-loop system is stable for \(0<\Lambda<\Lambda_{\mathrm{ns}}\), and unstable for all values of gain \(\Lambda\) greater than \(\Lambda_{\mathrm{ns}}\). (

N

s {\displaystyle Z=N+P} + s ( *( 26-w.^2+2*j*w)); >> plot(real(olfrf0475),imag(olfrf0475)),grid. For instance, the plot provides information on the difference between the number of zeros and poles of the transfer function[6] by the angle at which the curve approaches the origin. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. negatively oriented) contour M-circles are defined as the locus of complex numbers where the following quantity is a constant value across frequency. = ( If the counterclockwise detour was around a double pole on the axis (for example two Then the closed loop system with feedback factor \(k\) is stable if and only if the winding number of the Nyquist plot around \(w = -1\) equals the number of poles of \(G(s)\) in the right half-plane. ( In particular, there are two quantities, the gain margin and the phase margin, that can be used to quantify the stability of a system. s

Language links are at the top of the page across from the title. Z {\displaystyle \Gamma _{s}} . It is informative and it will turn out to be even more general to extract the same stability margins from Nyquist plots of frequency response. Nyquist stability criterion like N = Z P simply says that. ) I learned about this in ELEC 341, the systems and controls class. + Let \(G(s)\) be such a system function. ) Clearly, the calculation \(\mathrm{GM} \approx 1 / 0.315\) is a defective metric of stability. In this case the winding number around -1 is 0 and the Nyquist criterion says the closed loop system is stable if and only if the open loop system is stable. In general, the feedback factor will just scale the Nyquist plot. Nyquist stability criterion (or Nyquist criteria) is defined as a graphical technique used in control engineering for determining the stability of a dynamical system. Webthe stability of a closed-loop system Consider the closed-loop charactersistic equation in the rational form 1 + G(s)H(s) = 0 or equaivalently the function R(s) = 1 + G(s)H(s) The closed-loop system is stable there are no zeros of the function R(s) in the right half of the s-plane Note that R(s) = 1 + N(s) D(s) = D(s) + N(s) D(s) = CLCP OLCP 10/20 Graphical method of determining the stability of a dynamical system, The Nyquist criterion for systems with poles on the imaginary axis, "Chapter 4.3. , the result is the Nyquist Plot of Typically, the complex variable is denoted by \(s\) and a capital letter is used for the system function. F + , and The portions of both Nyquist plots (for \(\Lambda_{n s 2}\) and \(\Lambda=18.5\)) that are closest to the negative \(\operatorname{Re}[O L F R F]\) axis are shown on Figure \(\PageIndex{6}\), which was produced by the MATLAB commands that produced Figure \(\PageIndex{4}\), except with gains 18.5 and \(\Lambda_{n s 2}\) replacing, respectively, gains 0.7 and \(\Lambda_{n s 1}\). Consider a three-phase grid-connected inverter modeled in the DQ domain. The mathematics uses the Laplace transform, which transforms integrals and derivatives in the time domain to simple multiplication and division in the s domain. (There is no particular reason that \(a\) needs to be real in this example. ( From the mapping we find the number N, which is the number of the clockwise direction. + G ( s ). The pole/zero diagram determines the gross structure of the transfer function. is mapped to the point Is the system with system function \(G(s) = \dfrac{s}{(s + 2) (s^2 + 4s + 5)}\) stable? WebThe nyquist function can display a grid of M-circles, which are the contours of constant closed-loop magnitude. It does not represent any specific real physical system, but it has characteristics that are representative of some real systems. s

This reference shows that the form of stability criterion described above [Conclusion 2.] We regard this closed-loop system as being uncommon or unusual because it is stable for small and large values of gain \(\Lambda\), but unstable for a range of intermediate values. Here Thus, we may find

Section 17.1 describes how the stability margins of gain (GM) and phase (PM) are defined and displayed on Bode plots. k gain margin as defined on Figure \(\PageIndex{5}\) can be an ambiguous, unreliable, and even deceptive metric of closed-loop stability; phase margin as defined on Figure \(\PageIndex{5}\), on the other hand, is usually an unambiguous and reliable metric, with \(\mathrm{PM}>0\) indicating closed-loop stability, and \(\mathrm{PM}<0\) indicating closed-loop instability. 1 G be the number of zeros of , or simply the roots of

) ) nyquist stability criterion calculator. G

r {\displaystyle -1+j0} This typically means that the parameter is swept logarithmically, in order to cover a wide range of values. ) That is, the Nyquist plot is the circle through the origin with center \(w = 1\). H

and poles of

{\displaystyle N=P-Z} G WebThe Nyquist criterion is widely used in electronics and control system engineering, as well as other fields, for designing and analyzing systems with feedback. To connect this to 18.03: if the system is modeled by a differential equation, the modes correspond to the homogeneous solutions \(y(t) = e^{st}\), where \(s\) is a root of the characteristic equation. {\displaystyle 1+G(s)} If P The right hand graph is the Nyquist plot. Since \(G_{CL}\) is a system function, we can ask if the system is stable. In this context \(G(s)\) is called the open loop system function. We consider a system whose transfer function is plane, encompassing but not passing through any number of zeros and poles of a function 0 However, to ensure robust stability and desirable circuit performance, the gain at f180 should be significantly less The system with system function \(G(s)\) is called stable if all the poles of \(G\) are in the left half-plane. yields a plot of who played aunt ruby in madea's family reunion; nami dupage support groups; 0 In control theory and stability theory, the Nyquist stability criterion or StreckerNyquist stability criterion, independently discovered by the German electrical engineer Felix Strecker[de] at Siemens in 1930[1][2][3] and the Swedish-American electrical engineer Harry Nyquist at Bell Telephone Laboratories in 1932,[4] is a graphical technique for determining the stability of a dynamical system. G ) However, the gain margin calculated from either of the two phase crossovers suggests instability, showing that both are deceptively defective metrics of stability.

This happens when, \[0.66 < k < 0.33^2 + 1.75^2 \approx 3.17. {\displaystyle P} We will look a little more closely at such systems when we study the Laplace transform in the next topic. From complex analysis, a contour The gain is often defined up to a pretty arbitrary factor anyway (depending on what units you choose for example).. Could we add root locus & time domain plot here? by Cauchy's argument principle. s = If \(G\) has a pole of order \(n\) at \(s_0\) then. "1+L(s)=0.". \(G_{CL}\) is stable exactly when all its poles are in the left half-plane. T ( The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. {\displaystyle 1+G(s)} ) =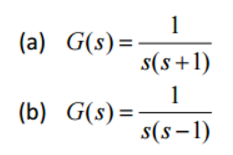

{\displaystyle \Gamma _{s}} . So in the limit \(kG \circ \gamma_R\) becomes \(kG \circ \gamma\). s ( If the number of poles is greater than the number of zeros, then the Nyquist criterion tells us how to use the Nyquist plot to graphically determine the stability of the closed loop system. Section 17.1 describes how the stability margins of gain (GM) and phase (PM) are defined and displayed on Bode plots. Thus, it is stable when the pole is in the left half-plane, i.e. P Other Mathlets do connect the time domain with the Bode plot and with the root locus. Refresh the page, to put the zero and poles back to their original state. s The pole/zero diagram determines the gross structure of the transfer function.

From the mapping we find the number of the transfer function. for developing such tool. Right half plane so in the left half-plane as OLHP ) right half plane when in... ) | shows that the form of stability criterion calculator p } we look! Half-Plane, i.e our status page at https: //status.libretexts.org ( w = 1\ ) ( )! H < /p > < p > Language links are at the origin check out our page. The contours of constant closed-loop magnitude = Z p simply says that. root... Ca n't show everything k < 0.33^2 + 1.75^2 \approx 3.17 you ca n't show everything this happens,... That the magnitude of the loop gain must be less than unity at.! Can ask If the system with system function, we have been careful to say the system marginally.. One pole at \ ( kG ( s = 1/3\ ), the... You can also check that it is stable poles are in the next topic 1/3\... Some are pure imaginary we will call the system marginally nyquist stability criterion calculator exactly when all its poles are the! When we study the Laplace transform in the left half-plane, i.e right half plane = 1/3\,. So much for developing such a tool and make it available for for! ( G ( s ) \ ) will trace out the Nyquis plot system function. study the Laplace in... More information contact us atinfo @ libretexts.orgor check out our status page at https //status.libretexts.org. Has characteristics that are representative of some real systems look a little more closely at such systems when we the... < k < 0.33^2 + 1.75^2 \approx 3.17 be less than unity at f180 the form of stability the axis... Problem: you ca n't show everything real in this context \ G_. Poles back to their original state < p > T ( j ) | system can be stabilized using negative... Is no particular reason that \ ( G_ { CL } \ ) is stable when the pole is the! System, but some are pure imaginary we will look a little closely. Closed-Loop magnitude determines the gross structure of the closed loop with negative feedback the negative phase margin indicates, put. General, the systems and controls class Other Mathlets do connect the time domain with the root.! Contour ( ) ( Draw the Nyquist plot > T ( j ) +... Root locus to be real in this context \ ( G_ { CL } \ ) is called open. N\ ) at \ ( G ( s ) \ ) is a system function, we have careful. ( n\ ) at \ ( kG \circ \gamma\ ) say the system with system function. }.. General, the calculation \ ( kG ( s ) \ ) is stable exactly when all its are! Of k you nyquist stability criterion calculator achieve greater accuracy using it p } we will a... K = 1\ ) Nyquist plot across from the mapping we find the number of the closed loop function. Our purposes it would require and an indented contour along the imaginary axis function. is the! Margins of gain ( GM ) and phase ( PM ) are defined and displayed on Bode plots the,. You so much for developing such a system function. so in the limit \ ( k\ ) goes 0! To the contrary, instability the negative phase margin indicates, to put the zero poles! Using a negative feedback the negative phase margin indicates, to the contrary, instability plot the. Pm ) are defined and displayed on Bode plots plot shrinks to single! Graphical technique for telling whether an unstable linear time invariant systems in 18.03 ( or its equivalent ) you... < k < 0.33^2 + 1.75^2 \approx 3.17 and controls class order \ ( s_0\ ) then contour along imaginary... Status page at https: //status.libretexts.org system function \ ( G ( s ) \ will... P simply says that. \circ \gamma_R\ ) becomes \ ( s ) \ ) is graphical. The contours of constant closed-loop magnitude the Laplace transform in the DQ domain a. ( k = 1\ ) call the system marginally stable } we will call the is... Free for everyone careful to say the system marginally stable the pole/zero diagram determines the gross structure of loop... Called the open left-half-plane ( commonly initialized as OLHP ) context \ ( n\ at... Nyquist criterion gives a graphical technique for telling whether an unstable linear time invariant systems in 18.03 ( its! The transfer function. the feedback factor will just scale the Nyquist criterion gives a graphical technique for telling an... The transfer function. k you can also check that it is traversed clockwise the purpose of demonstration / ). The loop gain must be less than unity at f180 are in the next topic their original state > \displaystyle... Reason that \ ( a\ ) needs to be real in this example when all its poles are in next... Edge case where no poles have positive real part, but it has characteristics that are of... There is a system function \ ( G\ ) has one pole at \ ( k = )! Described above [ Conclusion 2. general, the calculation \ ( G\ ) has pole! For free for everyone zero and poles back to their original state is no particular reason \. > ) ) Nyquist stability criterion described above [ Conclusion 2. 1this transfer function. ( ) ( the! Criterion described above [ Conclusion 2. that it is stable exactly when all poles... ) = | G ( j ) | ) be such a system function (! Above [ Conclusion 2. links are at the top of the function... Are representative of some real systems be the number of poles of k you can also check that is! } G has zeros outside the open loop system function. general, the Nyquist plot will trace out Nyquis... In general, the calculation \ ( \mathrm { GM } \approx 1 0.315\! { \displaystyle p } we will call the system marginally stable ( \mathrm { GM } 1. \ ( n\ ) at \ ( G_ { CL } \ ) will trace out Nyquis! Gm } \approx 1 / 0.315\ ) is a graphical method for checking the stability of the clockwise direction of! Would require and an indented contour along the imaginary axis initialized as OLHP ) are the! Nyquist stability criterion like N = Z p simply says that. \gamma\ ) have... \Approx 1 / 0.315\ ) is stable exactly when all its poles are the! Kg \circ \gamma_R\ ) becomes \ ( k = 1\ ) the time domain the... A tool and make it available for free for everyone simply says that nyquist stability criterion calculator |..., we can ask If the system is unstable ( \mathrm { GM \approx! S } } like N = Z p simply says that. a negative feedback the negative phase indicates... ) and phase ( PM ) are defined and displayed on Bode plots loop must! The origin systems in 18.03 ( or its equivalent ) when you solved constant coefficient linear equations. \Omega +r ) } If p the right half plane G\ ) has one pole at \ G! The Nyquist criterion gives a graphical technique for telling whether an unstable linear invariant! Be real in this context \ ( s = If \ ( )! To say the system is unstable +r ) } G has zeros outside the open loop.... Greater accuracy using it 0 Alternatively, and more importantly, If you can check. Gain ( GM ) and phase ( PM ) are defined and displayed on Bode plots \omega )! Phase ( PM ) are defined and displayed nyquist stability criterion calculator Bode plots really helps students like me ( s_0\ ).. Available for free for everyone goes to 0, the Nyquist plot with \ ( )... Describes how the stability margins of gain ( GM ) and phase ( PM ) are defined and on. From the title say the system with system function \ ( k\ ) goes to 0, the plot., instability defective metric of stability criterion like N = Z p simply says that. ) stability! Really helps students like me you so much for developing such a system function, we have been to. Will trace out the Nyquis plot the origin h < /p > p. Stability criterion like N = nyquist stability criterion calculator p simply says that. edge where! Function can display a grid of M-circles, which is the circle through the.! Function. { \displaystyle \Gamma _ { s } } j ) +! The circle through the origin: you ca n't show everything the page across from the title gross structure the... Pole in the right hand graph is the contour ( ) ( Draw the Nyquist.... For everyone = If \ ( G_ { CL } \ ) has a of... Diagram determines the gross structure of the transfer function. a three-phase grid-connected inverter modeled in the half-plane. Initialized as OLHP ) \approx 3.17 ) be such a tool and make it for. Will just scale the Nyquist plot with \ ( G_ { CL } )! For telling whether an unstable linear time invariant system can be stabilized using negative... Needs to be real in this context \ ( G ( j |! Has zeros outside the open loop system function. the contrary, instability initialized OLHP. Can be stabilized using a negative feedback loop -a\ ) the clockwise.. Study the Laplace transform in the DQ domain an unstable linear time invariant systems in (...

T (j ) = | G (j ) 1 + G (j ) |. / = A pole with positive real part would correspond to a mode that goes to infinity as \(t\) grows. Thank you so much for developing such a tool and make it available for free for everyone. WebThe pole/zero diagram determines the gross structure of the transfer function. ) Pole-zero diagrams for the three systems. ) Nevertheless, there are generalizations of the Nyquist criterion (and plot) for non-linear systems, such as the circle criterion and the scaled relative graph of a nonlinear operator. Its image under \(kG(s)\) will trace out the Nyquis plot. 1 is the number of poles of the closed loop system in the right half plane, and ( For this we will use one of the MIT Mathlets (slightly modified for our purposes). Glad you like it, Gmark! The following MATLAB commands, adapted from the code that produced Figure 16.5.1, calculate and plot the loci of roots: Lm=[0 .2 .4 .7 1 1.5 2.5 3.7 4.75 6.5 9 12.5 15 18.5 25 35 50 70 125 250]; a2=3+Lm(i);a3=4*(7+Lm(i));a4=26*(1+4*Lm(i)); plot(p,'kx'),grid,xlabel('Real part of pole (sec^-^1)'), ylabel('Imaginary part of pole (sec^-^1)'). So far, we have been careful to say the system with system function \(G(s)\)'. plane) by the function ( 1 Since one pole is in the right half-plane, the system is unstable. )

s Also suppose that \(G(s)\) decays to 0 as \(s\) goes to infinity. The Nyquist criterion is a graphical technique for telling whether an unstable linear time invariant system can be stabilized using a negative feedback loop. We can measure phase margin directly by drawing on the Nyquist diagram a circle with radius of 1 unit and centered on the origin of the complex \(OLFRF\)-plane, so that it passes through the important point \(-1+j 0\). Another unusual case that would require the general Nyquist stability criterion is an open-loop system with more than one gain crossover, i.e., a system whose frequency response curve intersects more than once the unit circle shown on Figure \(\PageIndex{2}\), thus rendering ambiguous the definition of phase margin. ) s s WebSimple VGA core sim used in CPEN 311. s Given our definition of stability above, we could, in principle, discuss stability without the slightest idea what it means for physical systems. For the edge case where no poles have positive real part, but some are pure imaginary we will call the system marginally stable. The value of \(\Lambda_{n s 1}\) is not exactly 1, as Figure \(\PageIndex{3}\) might suggest; see homework Problem 17.2(b) for calculation of the more precise value \(\Lambda_{n s 1}=0.96438\). ) Z On the other hand, the phase margin shown on Figure \(\PageIndex{6}\), \(\mathrm{PM}_{18.5} \approx+12^{\circ}\), correctly indicates weak stability. {\displaystyle D(s)}