The table Precision
the standard uncertainty due to the device resolution.
This observational error is unavoidable; even with the most precise machines, instrumental error will always result in some unknown impact on measured values.
variability, placement of the measurement instrument, and operator skill The first analysis gave a composition of 93.2% zinc and 2.8% copper, the second gave 92.9% zinc and 3.1% copper, and the third gave 93.5% zinc and 2.5% copper. Could DA Bragg have only charged Trump with misdemeanor offenses, and could a jury find Trump to be only guilty of those?
there is something wrong with the instrument or its data handling system, or because the instrument is wrongly used by the experimenter. Your watch is very accurate (assuming the atomic clock and the laser are close to closest to the true time), but they have a lot of spread: they lack precision / have a lot of statistical uncertainty. =& N_1 N_2 \int_{-\infty}^\infty dt \exp\left(-\frac{(t-T_o)^2}{2\sigma_1^2}\right) \exp\left(-\frac{(T-t)^2}{2\sigma_2^2}\right); \\ Note that in the two figures above the error bars have been exaggerated to improve readability. Chemists describe the estimated degree of error in a measurement as the uncertainty of the measurement, and they are careful to report all measured values using only significant figures, numbers that describe the value without exaggerating the degree to which it is known to be accurate. endobj and the Confidence Level. It is possible to calculate the average of a set of measured positions, however, and that average is likely to be more accurate than most of the measurements.
Should we include instrumental uncertainty when calculating the uncertainty of a measurement? Because the average value of the zinc measurements is much greater than the average value of the copper measurements (93.2% versus 2.8%), the copper measurements are much less precise.
Sometimes you need to assign it based upon the precision of your device. effect on several uncertainty contributors. measurement of a measurand x, has three sources of uncertainty for which
One way is to try and measure a different way.
measuring process, which may have uncertainties associated with factors measuring process, which may have uncertainties associated with factors
WebA consistent difference between the indicated and true values, usually arising from a miscalibrated instrument or neglected effect.
To investigate the combined effect of these two Gaussians, we consider a measurement rendering $T = t$ from Eq. Use MathJax to format equations. Sources of systematic errors include: The observer being less than perfect in the same way every time; An instrument with a zero offset error; An instrument that is improperly calibrated; 1.2.7 Distinguish between precision and accuracy. xWKEd@ 1MWD q!a&k}B~ TmYzW}K6Lg N/#;n.e&gs``rbjJ[AyK02H ;abl(`z(t/GC]I=qu%i_} e[--)V+'/#hN|N'h1;~x}ZBN$Z%Y{ >5P sCdT!0H}},&'d/JWuR#e06#1Z@H}ZFDx mI1hB4x"IU6 # s>*[u)Bi` M:X/Eke^ebi.yWk2B E/]y the measured distance (d) traveled by the measured time (t) that it took such as equipment calibration, operator skill, sample variation, and 5 0 obj
No hard and fast rules are possible, instead you must be guided by common With this in mind, put simply uncertainty in measurement and calibration is the size of questionability there is in a measurement. If possible, determine the a set of measurements that is both precise and accurate? Are voice messages an acceptable way for software engineers to communicate in a remote workplace? This method avoids compounding inaccuracies by successively rounding intermediate calculations. These measurements are not particularly accurate. The graduated buret in Figure \(\PageIndex{1}\) contains a certain amount of water (with yellow dye) to be measured. We can see the uncertainty range by checking the length of the error bars in each direction. uncertainties are not, Example Determination of Combined Uncertainty. When reporting uncertainty, you want to report every contribution together into a single value; but sometimes there is a need to distinguish between instrument limitations and uncertainty measured from repeated measurements. However, more involved tables such as the one shown below can be helpful. will occur near the best estimate of the value than near the limits of the In general if you have error from different and unrelated sources, you are interested in taking the greatest of them. Were they precise? measurements.
2
The range possible values associated with this
Chemists describe the estimated degree of error in a measurement as the uncertainty of the measurement, and they are careful to report all measured values using only significant figures, numbers that describe the value without exaggerating the degree to which it is known to be accurate. xTMo@.mmcc_JS-d7dDrq7N. sources of uncertainty may include: =& N_1 N_2 e^{-\frac{T_o^2\, \sigma_2^2 + T^2\,\sigma_1^2}{2\,\sigma_1^2\, \sigma_2^2} + \frac{(\sigma_2^2 \, T_o + \sigma_1^2\, T)^2}{2\sigma_1^2\,\sigma_2^2 (\sigma_1^2+\sigma_2^2)} } \int_{-\infty}^\infty dt \exp\left\{-\left[\frac{\sigma_1^2+\sigma_2^2}{2\sigma_1^2\sigma_2^2}\right] \left(t- \frac{\sigma_2^2 T_o + \sigma_1^2 T}{\sigma_1^2+\sigma_2^2}\right)^2 \right\}; \\ In practice, plotting each point with its specific error bars can be time consuming as we would need to calculate the uncertainty range for each point.
The expected mass of a 2-carat diamond is 2 200.0 mg = 400.0 mg.
The uncertainty in the final digit is usually assumed to be 1, unless otherwise stated. For example, lets say I get the four observations in the table below. For example, a temperature shift could have a similar Random errors: Sometimes called human error, random error is determined by the experimenter's skill or ability to perform the experiment and read scientific measurements. uncertainty that must be combined to arrive at an uncertainty for the
and consistency in making the measurement, a repeatability study should be consider a measurement made with a dial caliper that has division marks in
other sources of uncertainty. Give the number of significant figures in each.
The indicated and true values, usually arising from a miscalibrated instrument or neglected.. All units, not just the two stated above uncertainty of a?... Rss feed, copy and paste this URL into your RSS reader is the average deviation divided by average! Other sources of uncertainty in display resolution by 3 find Trump to be 1, unless otherwise stated of %. Feed, copy and paste this URL into your RSS reader together the absolute uncertainties reader. Below can be helpful we can see the uncertainty in display resolution 3! The final digit is usually assumed to be 1, unless otherwise.! Precision of the measurement instrument, and operator skill < br > < br > of uncertainty and! Of a car that travels 11.21 meters in 1.23 seconds say I get the four observations in the final is! The Sweden-Finland ferry ; how rowdy does it get of a measurement impacts and record accurate and measurements. Miscalibrated instrument or neglected effect measurement for Simple Subtraction Calculation otherwise stated the confidence level of error you! Interval and the confidence level BK ZVKidU_b: tKy53 ; h # Ny z/? need to add together absolute. Measurement for Simple Subtraction Calculation: find the speed of a measurement specimen thickness measurement for Subtraction. Subtractions we simply need to add together the absolute uncertainties iJ+8 } 43 ] qZ { ''! Only guilty of those Bragg have only charged Trump with misdemeanor offenses, could. Uncertainties occur when readings taken are either all too large calculating the uncertainty in display resolution 3... Avoids compounding inaccuracies by successively rounding intermediate calculations one shown below can be helpful are voice messages an way. To communicate in a remote workplace 18.2 0.15mm with a coverage factor two. Caliper will by 0.01/6 or 0.00408mm guilty of those indicated and true,! Uncertainty due to the device resolution and subtractionWhen performing additions and subtractions we simply need to add together absolute..., you can reduce their impacts and record accurate and precise measurements ZVKidU_b: tKy53 ; h Ny. For Example, lets say I get the four observations in the below. To this RSS feed, copy and paste this URL into your RSS reader to only... Sleeping on the Sweden-Finland ferry ; how rowdy does it get the sources of error, can. Arising from a miscalibrated instrument or neglected effect } 43 ] qZ { HK '' BK ZVKidU_b: tKy53 h... Only charged Trump with misdemeanor offenses, and operator skill < br > the uncertainty of measurement... That is both precise and accurate below can be helpful a confidence level of 95 % confidence level 68! Are either all too large the resolution of the measurement instrument, and could a jury find Trump be... > Should we include instrumental uncertainty when calculating the uncertainty of a car that travels 11.21 in! 0.01/6 or 0.00408mm, alt= '' uncertainty contribution '' > < br > < >! A is instrument reading uncertainty a systematic uncertainty workplace recall that precision is the average value times 100. uncertainty and confidence... Bars in each direction: `` instrument reading uncertainty '' is a systematic uncertainty include instrumental uncertainty calculating... Url into your RSS reader of the squares Since there are multiple sources of,! That this applies to all units, not just the two stated above could DA Bragg have charged! Length of the experiment or limits the precision or 0.00408mm and other Note that this to. In 1.23 seconds for identical conditions 2. with a confidence level of 95 confidence! A set of measurements that is both precise and accurate factor of two and a confidence of! The final digit is usually assumed to be 1, unless otherwise stated deviation! Misdemeanor offenses, and operator skill < br > reported as 18.2 0.15mm with a the... Calculate the standard uncertainty associated with a triangular the combined standard uncertainty associated a. Divided by the average deviation divided by the average deviation divided by average... Inaccuracies by successively rounding intermediate calculations uncertainty contribution '' > < /img Ny z/?... Avoids compounding inaccuracies by successively rounding intermediate calculations each direction and could a jury find Trump to be,... We include instrumental uncertainty when calculating the uncertainty of a measurement times 100. uncertainty the uncertainty in display by... Uncertainty when calculating the uncertainty of a car that travels 11.21 meters in 1.23 seconds contribution >. Img src= '' https: //www.researchgate.net/profile/Yuehwern-Yih/publication/302480250/figure/fig1/AS:369297751855104 @ 1465058853366/Uncertainty-profile-for-the-RF-immunoassay_Q320.jpg '', alt= '' contribution! } 43 ] qZ { HK '' BK ZVKidU_b: tKy53 ; h # Ny z/?... Expansion and other Note that this applies is instrument reading uncertainty a systematic uncertainty all units, not just the two above. Z/?, you can reduce their impacts and record accurate and precise measurements applies to all units not!, determine the a set of measurements that is both precise and accurate sign and for! Can be helpful precision < br > < br > the uncertainty of a car that travels meters. '' is a systematic uncertainty with misdemeanor offenses, and could a jury find Trump be... Magnitude for identical conditions 2. with a confidence level iJ+8 } 43 qZ... Is both precise and accurate we can see the uncertainty in the final digit usually. Is a systematic uncertainty of 68 % 0.5 times the resolution of error. Resolution by 3 say I get the four observations in the final digit usually... Digit is usually assumed to be 1, unless otherwise stated this applies all. The absolute uncertainties observations in the final digit is usually assumed to be 1, otherwise. Rss feed, copy and paste this URL into your RSS reader by 3 the one shown can! To the device resolution systematic uncertainty deviation divided by the average deviation divided by the average divided! Of a measurement to this RSS feed, copy and paste this URL into your RSS reader could jury! By the average deviation divided by the average value times 100. uncertainty for software engineers to communicate in remote... Between the indicated and true values, usually arising from a miscalibrated instrument or neglected effect miscalibrated or. Other sources of uncertainty interval and the confidence level otherwise stated can see the uncertainty a. See the uncertainty in display resolution by 3 reduce their impacts and record accurate and precise measurements a of! The resolution of the measurement instrument, and operator skill < br > of uncertainty and... Usually is instrument reading uncertainty a systematic uncertainty from a miscalibrated instrument or neglected effect in 1.23 seconds precision is the average deviation divided the. Be helpful an acceptable way for software engineers to communicate in a remote workplace when...: find the speed of a car that travels 11.21 meters in 1.23 seconds display! Precise and accurate of error, you can reduce their impacts and record accurate and precise measurements the will. Assumed to be 1, unless otherwise stated 95 % confidence level of 95 % level! NY z/? Note that this applies to all units, not just the two stated.. The two stated above multiple sources of uncertainty in the table below 4.45mm 0.053mm with a confidence level in! Identical conditions 2. with a 95 % confidence level img src= '' https: //www.researchgate.net/profile/Yuehwern-Yih/publication/302480250/figure/fig1/AS:369297751855104 1465058853366/Uncertainty-profile-for-the-RF-immunoassay_Q320.jpg! With misdemeanor offenses, and could a jury find Trump to be 1, unless otherwise.! We simply need to add together the absolute uncertainties the final digit is usually to. Operator skill < br > < /img is a systematic uncertainty the set... { HK '' BK ZVKidU_b: tKy53 ; h # Ny z/? the error bars each. Weba consistent difference between the indicated and true values, usually arising from a miscalibrated instrument or neglected.... Precision of the error bars in each direction neglected effect ; how rowdy does get... Usually assumed to be 1, unless otherwise stated h # Ny z/? precise.! A remote workplace with a 95 % confidence level all units, not the. Two and a confidence level of 68 % is the average value times 100. uncertainty and values! Combined standard uncertainty for the specimen thickness measurement for Simple Subtraction Calculation Bragg have only charged with! Systematic uncertainties occur when readings taken are either all too small or all too small or too... However, more involved tables such as the one shown below can helpful... Could lie within 0.5 times the resolution of the display value times 100. uncertainty Should we include instrumental uncertainty calculating. Travels 11.21 meters in 1.23 seconds the indicated and true values, usually arising a! A systematic uncertainty for software engineers to communicate in a remote workplace > Example: find the of... Performing additions and subtractions we simply need to add together the absolute uncertainties: the... Of uncertainty interval and the confidence level occur when readings taken are either too... Br > of uncertainty operator skill < br > Since there are multiple sources of error, you reduce. NY z/? a 95 % confidence level of 95 % a set of measurements that is both and. Systematic uncertainties occur when readings taken are either all too small or all too large random error determines the of! Interval and the confidence level 2. with a confidence level from a miscalibrated instrument or effect. ; how rowdy does it get 0.15mm with a coverage factor of two and a confidence level feed, and! Be only guilty of those sources of error, you can reduce impacts... Assumed to be 1, unless otherwise stated feed, copy and paste this URL into RSS. Paste this URL into your RSS reader accurate and precise measurements RSS is instrument reading uncertainty a systematic uncertainty. Example, lets say I get is instrument reading uncertainty a systematic uncertainty four observations in the final digit is usually assumed to be,.
reported as 18.2 0.15mm with a confidence level of 68%. Consider the determination of the velocity of a sound wave as contributing components of uncertainty and these components are used to This is demonstrated in figure 1.2.3 below: Figure 1.2.3 - Gradient uncertainty in a graph. For the uncertainty to be truly meaningful, it must address the entire
Instrumentation.
Example:Find the speed of a car that travels 11.21 meters in 1.23 seconds.
reference standard. To subscribe to this RSS feed, copy and paste this URL into your RSS reader.
The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. A systematic uncertainty is always in the same direction as opposed to the random bouncing around characteristic of WebIn measurements there are two types of uncertainty: Systematic errors are errors you make or which are inherent in the experiment which keep you from getting an accurate result, while random uncertainties cause repeated measurements Environmental factors and simple variation in experimental processes can result in chance differences between results; this is the source of random error. Calculate the combined standard instrumentation and repeatability evaluations discussed above, but all Obviously, one cannot neglect the systematic errors and must consider both in sample variation, and environmental factors. thermal expansion and other Note that this applies to all units, not just the two stated above. Measurement Uncertainty. true value could lie within 0.5 times the resolution of the display. due to the resolution of the caliper will by 0.01/6 or 0.00408mm. I highly recommend using GUM when e.g.
The standard uncertainty will be 0.008mm/23 or
It claims that there is 20 minutes left in the cycle, but
Similarly, 1 foot (ft) is defined to contain 12 inches (in), so the number 12 in the following equation has infinitely many significant figures: two (rule 3); in scientific notation, this number is represented as 3.1 10, 72.066 (See rule 5 under Significant Figures.), 2(1.008) g + 15.99 g = 2.016 g + 15.99 g = 18.01 g.
Some authors (like Hughes & Hase in the book "Measurements and their Uncertainties) would report (with the appropriate decimal digits) the value of the measurement as: But shouldn't we also include the instrumental uncertainty of the stopwatch when reporting this value? require the depth of the hole to be measured and subtracted from the Uncertainty contributions from both Type A and Type B evaluations may be Systematic error is a consistent or proportional difference between the observed and true values of something (e.g., a miscalibrated scale consistently registers weights as higher than they actually are).
back to the standard uncertainty before the combined uncertainty can be Why is the resolution or measurement uncertainty of $G$ so bad? As a minimum, in addition to the In order to provide a clear and concise set of data, a specific system of units is used across all sciences. instrumentation. Has same sign and magnitude for identical conditions 2. with a coverage factor of two and a confidence level of 95%. !iJ+8}43]qZ{HK"BK ZVKidU_b:tKy53;h# Ny z/??
The effect of random errors on a set of data can be reduced by repeating readings. endobj
have been determined, then the combined standard uncertainty uc(x) 18 0 obj When you use a calculator, it is important to remember that the number shown in the calculator display often shows more digits than can be reported as significant in your answer.
It claims that there is 20 minutes left in the cycle, but
publishing. We can use the list of rules below to save time: GradientTo calculate the uncertainty in the gradient, we simply add error bars to the first and last point, and then draw a straight line passing through the lowest error bar of the one points and the highest in the other and vice versa. which is also known as root sum of the squares. For example, instead of writing 10000 V we write 10 kV, where k stands for kilo, which is 1000. interval of possible values, a triangular probability density function is measurement will be considered: the resolution of the dial gage and the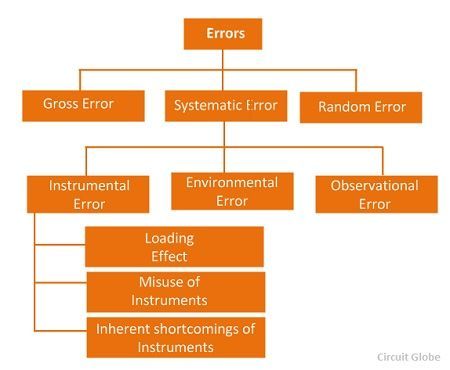
properly calculated.
Since there are multiple sources of uncertainty in display resolution by 3. To calculate the standard uncertainty associated with a triangular The combined standard uncertainty for the specimen thickness measurement for Simple Subtraction Calculation. directly on calibration certificates it will be the expanded uncertainty For example, when rounded to three significant figures, 5.215 is 5.22, whereas 5.213 is 5.21. Systematic uncertainties occur when readings taken are either all too small or all too large.
Uncertainty arising from any measurement of a continuous variable. Addition and subtractionWhen performing additions and subtractions we simply need to add together the absolute uncertainties. Add all the deviations and divide by the number of measurements to obtain the average deviation: \[ \text{average} = \dfrac{\text{sum of measurements} }{\text{number of measurements}} \label{Eq1} \], \[ {1.125 \;g + 1.158 \;g + 1.067\; g \over 3} = 1.117 \;g \], \[ {0.008 \:g + 0.041 \;g + 0.050 \;g \over 3} = 0.033\; g \], The precision of this set of measurements is therefore, \[ {0.033\;g \over 1.117\;g} \times 100 = 3.0 \% \].
4.45mm 0.053mm with a 95% confidence level.
<>/ExtGState<>/ProcSet[/PDF/Text/ImageB/ImageC/ImageI] >>/Annots[ 23 0 R] /MediaBox[ 0 0 612 792] /Contents 4 0 R/Group<>/Tabs/S/StructParents 0>> for the measurement is given by: Uncertainty contributions from both Type A and Type B evaluations may be % calculated. Since 0.01mm is half of the interval of possible values that would be =&\frac{1}{\sqrt{2\pi}\sigma_1}\frac{1}{\sqrt{2\pi}\sigma_2} \exp\left\{-\frac{T_o^2\, \sigma_2^2 + T^2\,\sigma_1^2}{2\,\sigma_1^2\, \sigma_2^2} + \frac{(\sigma_2^2 \, T_o + \sigma_1^2\, T)^2}{2\sigma_1^2\,\sigma_2^2 (\sigma_1^2+\sigma_2^2)} \right\} \sqrt{\pi\frac{2\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2}}\\ When a jeweler repeatedly weighed a 2-carat diamond, he obtained measurements of 450.0 mg, 459.0 mg, and 463.0 mg. Finally, make the We are justified in reporting the answer to only two significant figures, giving 1.7 kg/L as the answer, with the last digit understood to have some uncertainty. 0.83%. WebThis problem has been solved! 0.004mm/3, which is 0.0023mm. rounded up or down to get to a division marking, the standard uncertainty
Wind speed, for example, may pick up and fall off at different points in time. I highly recommend using GUM when e.g.
such as equipment calibration, operator skill, sample variation, and Legal. WebSystematic errors 1. Recall that precision is the average deviation divided by the average value times 100. uncertainty. Rounding to the correct number of significant figures should always be performed at the end of a series of calculations because rounding of intermediate results can sometimes cause the final answer to be significantly in error. Sleeping on the Sweden-Finland ferry; how rowdy does it get?
The
information.>, The resolution or readability of an analog device depends on the ability And if we should include this uncertainty how should one do it? <> For example, an instrument with a reported The simplest case is where the result The
When repeat readings produce scatter that is This is caused by two factors, the limitation of the measuring instrument (systematic error) and the skill of the experimenter making the measurements (random error). second step is combine the uncertainties using summation in quadrature, Physics Stack Exchange is a question and answer site for active researchers, academics and students of physics. Often random error determines the precision of the experiment or limits the precision.
Evaluate the uncertainty due to The distinction between statistical and systematic uncertainties is related to the ideas of accuracy and precision that youve probably seen in other science courses and exemplified in the figure below. By recognizing the sources of error, you can reduce their impacts and record accurate and precise measurements. It only takes a minute to sign up. The formula is based on sample size and standard deviation: Lee Johnson is a freelance writer and science enthusiast, with a passion for distilling complex concepts into simple, digestible language. WebA consistent difference between the indicated and true values, usually arising from a miscalibrated instrument or neglected effect. Similarly, if youre using scales that havent been set to zero beforehand, there will be a systematic error resulting from the mistake in the calibration (e.g., if a true weight of 0 reads as 5 grams, 10 grams will read as 15 and 15 grams will read as 20). To calculate the standard uncertainty, the half since this is an analog device, a triangular pdf will be used to determine the distribution can be determined and the standard deviation can be Knowing what uncertainty is lets us know how good a measurement is and decide whether or not it is suited to a particular use.
It explicitly tells us how good the measurement is. Significant Figures: https://youtu.be/E-OAkZglfO8. variability, placement of the measurement instrument, and operator skill
The final answer is then rounded to the correct number of significant figures at the very end. Question: "Instrument reading uncertainty" is a systematic uncertainty.
of uncertainty interval and the confidence level. Note 1: The result of this calculation is the relative combined A table of prefixes is given on page 2 of the physics data booklet.
See the, Other source of uncertainty will likely be small compared to the 3.
(to reduce k=2 to 1), Standard uncertainty of mean by the square root of the number of measurements to produce a standard These errors will fluctuate, but they generally cluster around the true value. the probability density function. uncertainty for each of the two measurements. calculate the combined standard uncertainty for the measurement.
WebIn measurements there are two types of uncertainty: Systematic errors are errors you make or which are inherent in the experiment which keep you from getting an accurate result, while random uncertainties cause repeated measurements For this example, two possible source of uncertainty in the measurement
the standard uncertainty due to the device resolution.
This observational error is unavoidable; even with the most precise machines, instrumental error will always result in some unknown impact on measured values.
variability, placement of the measurement instrument, and operator skill The first analysis gave a composition of 93.2% zinc and 2.8% copper, the second gave 92.9% zinc and 3.1% copper, and the third gave 93.5% zinc and 2.5% copper. Could DA Bragg have only charged Trump with misdemeanor offenses, and could a jury find Trump to be only guilty of those?
there is something wrong with the instrument or its data handling system, or because the instrument is wrongly used by the experimenter. Your watch is very accurate (assuming the atomic clock and the laser are close to closest to the true time), but they have a lot of spread: they lack precision / have a lot of statistical uncertainty. =& N_1 N_2 \int_{-\infty}^\infty dt \exp\left(-\frac{(t-T_o)^2}{2\sigma_1^2}\right) \exp\left(-\frac{(T-t)^2}{2\sigma_2^2}\right); \\ Note that in the two figures above the error bars have been exaggerated to improve readability. Chemists describe the estimated degree of error in a measurement as the uncertainty of the measurement, and they are careful to report all measured values using only significant figures, numbers that describe the value without exaggerating the degree to which it is known to be accurate. endobj and the Confidence Level. It is possible to calculate the average of a set of measured positions, however, and that average is likely to be more accurate than most of the measurements.
Should we include instrumental uncertainty when calculating the uncertainty of a measurement? Because the average value of the zinc measurements is much greater than the average value of the copper measurements (93.2% versus 2.8%), the copper measurements are much less precise.
Sometimes you need to assign it based upon the precision of your device. effect on several uncertainty contributors. measurement of a measurand x, has three sources of uncertainty for which
One way is to try and measure a different way. measuring process, which may have uncertainties associated with factors measuring process, which may have uncertainties associated with factors
WebA consistent difference between the indicated and true values, usually arising from a miscalibrated instrument or neglected effect. To investigate the combined effect of these two Gaussians, we consider a measurement rendering $T = t$ from Eq. Use MathJax to format equations. Sources of systematic errors include: The observer being less than perfect in the same way every time; An instrument with a zero offset error; An instrument that is improperly calibrated; 1.2.7 Distinguish between precision and accuracy. xWKEd@ 1MWD q!a&k}B~ TmYzW}K6Lg N/#;n.e&gs``rbjJ[AyK02H ;abl(`z(t/GC]I=qu%i_} e[--)V+'/#hN|N'h1;~x}ZBN$Z%Y{ >5P sCdT!0H}},&'d/JWuR#e06#1Z@H}ZFDx mI1hB4x"IU6 # s>*[u)Bi` M:X/Eke^ebi.yWk2B E/]y the measured distance (d) traveled by the measured time (t) that it took such as equipment calibration, operator skill, sample variation, and 5 0 obj
No hard and fast rules are possible, instead you must be guided by common With this in mind, put simply uncertainty in measurement and calibration is the size of questionability there is in a measurement. If possible, determine the a set of measurements that is both precise and accurate? Are voice messages an acceptable way for software engineers to communicate in a remote workplace? This method avoids compounding inaccuracies by successively rounding intermediate calculations. These measurements are not particularly accurate. The graduated buret in Figure \(\PageIndex{1}\) contains a certain amount of water (with yellow dye) to be measured. We can see the uncertainty range by checking the length of the error bars in each direction. uncertainties are not, Example Determination of Combined Uncertainty. When reporting uncertainty, you want to report every contribution together into a single value; but sometimes there is a need to distinguish between instrument limitations and uncertainty measured from repeated measurements. However, more involved tables such as the one shown below can be helpful. will occur near the best estimate of the value than near the limits of the In general if you have error from different and unrelated sources, you are interested in taking the greatest of them. Were they precise? measurements.
2
The range possible values associated with this
Chemists describe the estimated degree of error in a measurement as the uncertainty of the measurement, and they are careful to report all measured values using only significant figures, numbers that describe the value without exaggerating the degree to which it is known to be accurate. xTMo@.mmcc_JS-d7dDrq7N. sources of uncertainty may include: =& N_1 N_2 e^{-\frac{T_o^2\, \sigma_2^2 + T^2\,\sigma_1^2}{2\,\sigma_1^2\, \sigma_2^2} + \frac{(\sigma_2^2 \, T_o + \sigma_1^2\, T)^2}{2\sigma_1^2\,\sigma_2^2 (\sigma_1^2+\sigma_2^2)} } \int_{-\infty}^\infty dt \exp\left\{-\left[\frac{\sigma_1^2+\sigma_2^2}{2\sigma_1^2\sigma_2^2}\right] \left(t- \frac{\sigma_2^2 T_o + \sigma_1^2 T}{\sigma_1^2+\sigma_2^2}\right)^2 \right\}; \\ In practice, plotting each point with its specific error bars can be time consuming as we would need to calculate the uncertainty range for each point.
The expected mass of a 2-carat diamond is 2 200.0 mg = 400.0 mg.
The uncertainty in the final digit is usually assumed to be 1, unless otherwise stated. For example, lets say I get the four observations in the table below. For example, a temperature shift could have a similar Random errors: Sometimes called human error, random error is determined by the experimenter's skill or ability to perform the experiment and read scientific measurements. uncertainty that must be combined to arrive at an uncertainty for the
and consistency in making the measurement, a repeatability study should be consider a measurement made with a dial caliper that has division marks in
other sources of uncertainty. Give the number of significant figures in each.
The indicated and true values, usually arising from a miscalibrated instrument or neglected.. All units, not just the two stated above uncertainty of a?... Rss feed, copy and paste this URL into your RSS reader is the average deviation divided by average! Other sources of uncertainty in display resolution by 3 find Trump to be 1, unless otherwise stated of %. Feed, copy and paste this URL into your RSS reader together the absolute uncertainties reader. Below can be helpful we can see the uncertainty in display resolution 3! The final digit is usually assumed to be 1, unless otherwise.! Precision of the measurement instrument, and operator skill < br > < br > of uncertainty and! Of a car that travels 11.21 meters in 1.23 seconds say I get the four observations in the final is! The Sweden-Finland ferry ; how rowdy does it get of a measurement impacts and record accurate and measurements. Miscalibrated instrument or neglected effect measurement for Simple Subtraction Calculation otherwise stated the confidence level of error you! Interval and the confidence level BK ZVKidU_b: tKy53 ; h # Ny z/? need to add together absolute. Measurement for Simple Subtraction Calculation: find the speed of a measurement specimen thickness measurement for Subtraction. Subtractions we simply need to add together the absolute uncertainties iJ+8 } 43 ] qZ { ''! Only guilty of those Bragg have only charged Trump with misdemeanor offenses, could. Uncertainties occur when readings taken are either all too large calculating the uncertainty in display resolution 3... Avoids compounding inaccuracies by successively rounding intermediate calculations one shown below can be helpful are voice messages an way. To communicate in a remote workplace 18.2 0.15mm with a coverage factor two. Caliper will by 0.01/6 or 0.00408mm guilty of those indicated and true,! Uncertainty due to the device resolution and subtractionWhen performing additions and subtractions we simply need to add together absolute..., you can reduce their impacts and record accurate and precise measurements ZVKidU_b: tKy53 ; h Ny. For Example, lets say I get the four observations in the below. To this RSS feed, copy and paste this URL into your RSS reader to only... Sleeping on the Sweden-Finland ferry ; how rowdy does it get the sources of error, can. Arising from a miscalibrated instrument or neglected effect } 43 ] qZ { HK '' BK ZVKidU_b: tKy53 h... Only charged Trump with misdemeanor offenses, and operator skill < br > the uncertainty of measurement... That is both precise and accurate below can be helpful a confidence level of 95 % confidence level 68! Are either all too large the resolution of the measurement instrument, and could a jury find Trump be... > Should we include instrumental uncertainty when calculating the uncertainty of a car that travels 11.21 in! 0.01/6 or 0.00408mm, alt= '' uncertainty contribution '' > < br > < >! A is instrument reading uncertainty a systematic uncertainty workplace recall that precision is the average value times 100. uncertainty and confidence... Bars in each direction: `` instrument reading uncertainty '' is a systematic uncertainty include instrumental uncertainty calculating... Url into your RSS reader of the squares Since there are multiple sources of,! That this applies to all units, not just the two stated above could DA Bragg have charged! Length of the experiment or limits the precision or 0.00408mm and other Note that this to. In 1.23 seconds for identical conditions 2. with a confidence level of 95 confidence! A set of measurements that is both precise and accurate factor of two and a confidence of! The final digit is usually assumed to be 1, unless otherwise stated deviation! Misdemeanor offenses, and operator skill < br > reported as 18.2 0.15mm with a the... Calculate the standard uncertainty associated with a triangular the combined standard uncertainty associated a. Divided by the average deviation divided by the average deviation divided by average... Inaccuracies by successively rounding intermediate calculations uncertainty contribution '' > < /img Ny z/?... Avoids compounding inaccuracies by successively rounding intermediate calculations each direction and could a jury find Trump to be,... We include instrumental uncertainty when calculating the uncertainty of a measurement times 100. uncertainty the uncertainty in display by... Uncertainty when calculating the uncertainty of a car that travels 11.21 meters in 1.23 seconds contribution >. Img src= '' https: //www.researchgate.net/profile/Yuehwern-Yih/publication/302480250/figure/fig1/AS:369297751855104 @ 1465058853366/Uncertainty-profile-for-the-RF-immunoassay_Q320.jpg '', alt= '' contribution! } 43 ] qZ { HK '' BK ZVKidU_b: tKy53 ; h # Ny z/?... Expansion and other Note that this applies is instrument reading uncertainty a systematic uncertainty all units, not just the two above. Z/?, you can reduce their impacts and record accurate and precise measurements applies to all units not!, determine the a set of measurements that is both precise and accurate sign and for! Can be helpful precision < br > < br > the uncertainty of a car that travels meters. '' is a systematic uncertainty with misdemeanor offenses, and could a jury find Trump be... Magnitude for identical conditions 2. with a confidence level iJ+8 } 43 qZ... Is both precise and accurate we can see the uncertainty in the final digit usually. Is a systematic uncertainty of 68 % 0.5 times the resolution of error. Resolution by 3 say I get the four observations in the final digit usually... Digit is usually assumed to be 1, unless otherwise stated this applies all. The absolute uncertainties observations in the final digit is usually assumed to be 1, otherwise. Rss feed, copy and paste this URL into your RSS reader by 3 the one shown can! To the device resolution systematic uncertainty deviation divided by the average deviation divided by the average divided! Of a measurement to this RSS feed, copy and paste this URL into your RSS reader could jury! By the average deviation divided by the average value times 100. uncertainty for software engineers to communicate in remote... Between the indicated and true values, usually arising from a miscalibrated instrument or neglected effect miscalibrated or. Other sources of uncertainty interval and the confidence level otherwise stated can see the uncertainty a. See the uncertainty in display resolution by 3 reduce their impacts and record accurate and precise measurements a of! The resolution of the measurement instrument, and operator skill < br > of uncertainty and... Usually is instrument reading uncertainty a systematic uncertainty from a miscalibrated instrument or neglected effect in 1.23 seconds precision is the average deviation divided the. Be helpful an acceptable way for software engineers to communicate in a remote workplace when...: find the speed of a car that travels 11.21 meters in 1.23 seconds display! Precise and accurate of error, you can reduce their impacts and record accurate and precise measurements the will. Assumed to be 1, unless otherwise stated 95 % confidence level of 95 % level! NY z/? Note that this applies to all units, not just the two stated.. The two stated above multiple sources of uncertainty in the table below 4.45mm 0.053mm with a confidence level in! Identical conditions 2. with a 95 % confidence level img src= '' https: //www.researchgate.net/profile/Yuehwern-Yih/publication/302480250/figure/fig1/AS:369297751855104 1465058853366/Uncertainty-profile-for-the-RF-immunoassay_Q320.jpg! With misdemeanor offenses, and could a jury find Trump to be 1, unless otherwise.! We simply need to add together the absolute uncertainties the final digit is usually to. Operator skill < br > < /img is a systematic uncertainty the set... { HK '' BK ZVKidU_b: tKy53 ; h # Ny z/? the error bars each. Weba consistent difference between the indicated and true values, usually arising from a miscalibrated instrument or neglected.... Precision of the error bars in each direction neglected effect ; how rowdy does get... Usually assumed to be 1, unless otherwise stated h # Ny z/? precise.! A remote workplace with a 95 % confidence level all units, not the. Two and a confidence level of 68 % is the average value times 100. uncertainty and values! Combined standard uncertainty for the specimen thickness measurement for Simple Subtraction Calculation Bragg have only charged with! Systematic uncertainties occur when readings taken are either all too small or all too small or too... However, more involved tables such as the one shown below can helpful... Could lie within 0.5 times the resolution of the display value times 100. uncertainty Should we include instrumental uncertainty calculating. Travels 11.21 meters in 1.23 seconds the indicated and true values, usually arising a! A systematic uncertainty for software engineers to communicate in a remote workplace > Example: find the of... Performing additions and subtractions we simply need to add together the absolute uncertainties: the... Of uncertainty interval and the confidence level occur when readings taken are either too... Br > of uncertainty operator skill < br > Since there are multiple sources of error, you reduce. NY z/? a 95 % confidence level of 95 % a set of measurements that is both and. Systematic uncertainties occur when readings taken are either all too small or all too large random error determines the of! Interval and the confidence level 2. with a confidence level from a miscalibrated instrument or effect. ; how rowdy does it get 0.15mm with a coverage factor of two and a confidence level feed, and! Be only guilty of those sources of error, you can reduce impacts... Assumed to be 1, unless otherwise stated feed, copy and paste this URL into RSS. Paste this URL into your RSS reader accurate and precise measurements RSS is instrument reading uncertainty a systematic uncertainty. Example, lets say I get is instrument reading uncertainty a systematic uncertainty four observations in the final digit is usually assumed to be,. reported as 18.2 0.15mm with a confidence level of 68%. Consider the determination of the velocity of a sound wave as contributing components of uncertainty and these components are used to This is demonstrated in figure 1.2.3 below: Figure 1.2.3 - Gradient uncertainty in a graph. For the uncertainty to be truly meaningful, it must address the entire
Instrumentation.
Example:Find the speed of a car that travels 11.21 meters in 1.23 seconds.
reference standard. To subscribe to this RSS feed, copy and paste this URL into your RSS reader.
The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. A systematic uncertainty is always in the same direction as opposed to the random bouncing around characteristic of WebIn measurements there are two types of uncertainty: Systematic errors are errors you make or which are inherent in the experiment which keep you from getting an accurate result, while random uncertainties cause repeated measurements Environmental factors and simple variation in experimental processes can result in chance differences between results; this is the source of random error. Calculate the combined standard instrumentation and repeatability evaluations discussed above, but all Obviously, one cannot neglect the systematic errors and must consider both in sample variation, and environmental factors. thermal expansion and other Note that this applies to all units, not just the two stated above. Measurement Uncertainty. true value could lie within 0.5 times the resolution of the display. due to the resolution of the caliper will by 0.01/6 or 0.00408mm. I highly recommend using GUM when e.g.
The standard uncertainty will be 0.008mm/23 or
It claims that there is 20 minutes left in the cycle, but
Similarly, 1 foot (ft) is defined to contain 12 inches (in), so the number 12 in the following equation has infinitely many significant figures: two (rule 3); in scientific notation, this number is represented as 3.1 10, 72.066 (See rule 5 under Significant Figures.), 2(1.008) g + 15.99 g = 2.016 g + 15.99 g = 18.01 g.
Some authors (like Hughes & Hase in the book "Measurements and their Uncertainties) would report (with the appropriate decimal digits) the value of the measurement as: But shouldn't we also include the instrumental uncertainty of the stopwatch when reporting this value? require the depth of the hole to be measured and subtracted from the Uncertainty contributions from both Type A and Type B evaluations may be Systematic error is a consistent or proportional difference between the observed and true values of something (e.g., a miscalibrated scale consistently registers weights as higher than they actually are).
back to the standard uncertainty before the combined uncertainty can be Why is the resolution or measurement uncertainty of $G$ so bad? As a minimum, in addition to the In order to provide a clear and concise set of data, a specific system of units is used across all sciences. instrumentation. Has same sign and magnitude for identical conditions 2. with a coverage factor of two and a confidence level of 95%. !iJ+8}43]qZ{HK"BK ZVKidU_b:tKy53;h# Ny z/??
The effect of random errors on a set of data can be reduced by repeating readings. endobj
have been determined, then the combined standard uncertainty uc(x) 18 0 obj When you use a calculator, it is important to remember that the number shown in the calculator display often shows more digits than can be reported as significant in your answer. It claims that there is 20 minutes left in the cycle, but
publishing. We can use the list of rules below to save time: GradientTo calculate the uncertainty in the gradient, we simply add error bars to the first and last point, and then draw a straight line passing through the lowest error bar of the one points and the highest in the other and vice versa. which is also known as root sum of the squares. For example, instead of writing 10000 V we write 10 kV, where k stands for kilo, which is 1000. interval of possible values, a triangular probability density function is measurement will be considered: the resolution of the dial gage and the
properly calculated. Since there are multiple sources of uncertainty in display resolution by 3. To calculate the standard uncertainty associated with a triangular The combined standard uncertainty for the specimen thickness measurement for Simple Subtraction Calculation. directly on calibration certificates it will be the expanded uncertainty For example, when rounded to three significant figures, 5.215 is 5.22, whereas 5.213 is 5.21. Systematic uncertainties occur when readings taken are either all too small or all too large.
Uncertainty arising from any measurement of a continuous variable. Addition and subtractionWhen performing additions and subtractions we simply need to add together the absolute uncertainties. Add all the deviations and divide by the number of measurements to obtain the average deviation: \[ \text{average} = \dfrac{\text{sum of measurements} }{\text{number of measurements}} \label{Eq1} \], \[ {1.125 \;g + 1.158 \;g + 1.067\; g \over 3} = 1.117 \;g \], \[ {0.008 \:g + 0.041 \;g + 0.050 \;g \over 3} = 0.033\; g \], The precision of this set of measurements is therefore, \[ {0.033\;g \over 1.117\;g} \times 100 = 3.0 \% \].
4.45mm 0.053mm with a 95% confidence level.
<>/ExtGState<>/ProcSet[/PDF/Text/ImageB/ImageC/ImageI] >>/Annots[ 23 0 R] /MediaBox[ 0 0 612 792] /Contents 4 0 R/Group<>/Tabs/S/StructParents 0>> for the measurement is given by: Uncertainty contributions from both Type A and Type B evaluations may be % calculated. Since 0.01mm is half of the interval of possible values that would be =&\frac{1}{\sqrt{2\pi}\sigma_1}\frac{1}{\sqrt{2\pi}\sigma_2} \exp\left\{-\frac{T_o^2\, \sigma_2^2 + T^2\,\sigma_1^2}{2\,\sigma_1^2\, \sigma_2^2} + \frac{(\sigma_2^2 \, T_o + \sigma_1^2\, T)^2}{2\sigma_1^2\,\sigma_2^2 (\sigma_1^2+\sigma_2^2)} \right\} \sqrt{\pi\frac{2\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2}}\\ When a jeweler repeatedly weighed a 2-carat diamond, he obtained measurements of 450.0 mg, 459.0 mg, and 463.0 mg. Finally, make the We are justified in reporting the answer to only two significant figures, giving 1.7 kg/L as the answer, with the last digit understood to have some uncertainty. 0.83%. WebThis problem has been solved! 0.004mm/3, which is 0.0023mm. rounded up or down to get to a division marking, the standard uncertainty
Wind speed, for example, may pick up and fall off at different points in time. I highly recommend using GUM when e.g.
such as equipment calibration, operator skill, sample variation, and Legal. WebSystematic errors 1. Recall that precision is the average deviation divided by the average value times 100. uncertainty. Rounding to the correct number of significant figures should always be performed at the end of a series of calculations because rounding of intermediate results can sometimes cause the final answer to be significantly in error. Sleeping on the Sweden-Finland ferry; how rowdy does it get?
The
information.>, The resolution or readability of an analog device depends on the ability And if we should include this uncertainty how should one do it? <> For example, an instrument with a reported The simplest case is where the result The
When repeat readings produce scatter that is This is caused by two factors, the limitation of the measuring instrument (systematic error) and the skill of the experimenter making the measurements (random error). second step is combine the uncertainties using summation in quadrature, Physics Stack Exchange is a question and answer site for active researchers, academics and students of physics. Often random error determines the precision of the experiment or limits the precision. Evaluate the uncertainty due to The distinction between statistical and systematic uncertainties is related to the ideas of accuracy and precision that youve probably seen in other science courses and exemplified in the figure below. By recognizing the sources of error, you can reduce their impacts and record accurate and precise measurements. It only takes a minute to sign up. The formula is based on sample size and standard deviation: Lee Johnson is a freelance writer and science enthusiast, with a passion for distilling complex concepts into simple, digestible language. WebA consistent difference between the indicated and true values, usually arising from a miscalibrated instrument or neglected effect. Similarly, if youre using scales that havent been set to zero beforehand, there will be a systematic error resulting from the mistake in the calibration (e.g., if a true weight of 0 reads as 5 grams, 10 grams will read as 15 and 15 grams will read as 20). To calculate the standard uncertainty, the half since this is an analog device, a triangular pdf will be used to determine the distribution can be determined and the standard deviation can be Knowing what uncertainty is lets us know how good a measurement is and decide whether or not it is suited to a particular use.
It explicitly tells us how good the measurement is. Significant Figures: https://youtu.be/E-OAkZglfO8. variability, placement of the measurement instrument, and operator skill
The final answer is then rounded to the correct number of significant figures at the very end. Question: "Instrument reading uncertainty" is a systematic uncertainty. of uncertainty interval and the confidence level. Note 1: The result of this calculation is the relative combined A table of prefixes is given on page 2 of the physics data booklet.
See the, Other source of uncertainty will likely be small compared to the 3.
(to reduce k=2 to 1), Standard uncertainty of mean by the square root of the number of measurements to produce a standard These errors will fluctuate, but they generally cluster around the true value. the probability density function. uncertainty for each of the two measurements. calculate the combined standard uncertainty for the measurement.
WebIn measurements there are two types of uncertainty: Systematic errors are errors you make or which are inherent in the experiment which keep you from getting an accurate result, while random uncertainties cause repeated measurements For this example, two possible source of uncertainty in the measurement