This page titled 4.5: Exponential and Gamma Distributions is shared under a not declared license and was authored, remixed, and/or curated by Kristin Kuter. Second, if \(x\geq0\), then the pdf is \(\lambda e^{-\lambda x}\), and the cdf is given by $$F(x) = \int^x_{-\infty} f(t) dt = \int^x_0 \lambda e^{-\lambda t} dt = -e^{-\lambda t}\Big|^x_0 = -e^{-\lambda x} - (-e^0) = 1-e^{-\lambda x}.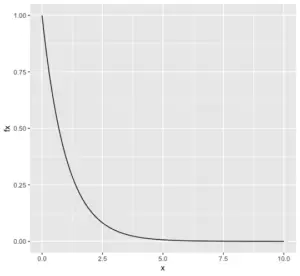 
You're asking about Exponential_distribution, the exponential distribution is the probability distribution that WebLorem ipsum dolor sit amet, consectetur adipis cing elit. Well this might confuse you. Whenever there is a case of 'At most' take all the outcomes which are either equal to the given and less than that. Sa Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. \implies& E\left(\frac{n-1}{n}\hat\lambda\right) = \lambda Webf (x) = And at x = 0 on the blue curve, we can see that f (x) = f (0) = 1 f (x) = Thus and , and as expected. Suppose that X_T = theta_0 + sigma t n=1 element_n (t = 1, 2, ) where theta_0 is a model parameter, and element_1, element_2, are independent and identically distributed random variables with mean 0 and variance sigma2e. n (another way to say this is that the X_i form a random sample from an exponential distribution with.
Let Z = X / Y. Determine the (a) mean and (b) variance of X. a. Based on the given data, determine the exponential distribution. (a) Show that ln L(lambda) = -n lambda + (sigma x_i) ln lambda - ln(x_1! Let X, Y be independent exponential random variables with parameters lambda and mu respectively.
. 0, & \text{otherwise.} Even though it is almost the same as exponential distribution, we usually called negative due to the negative sign of the exponent. Find the mean function for. Let X_1, X_2, , X_n be a random sample from a Gamma distribution with parameters alpha = 2 and beta = theta . Show the mean and variance are given by the fol. (ii.) The continuous random variable \(X\) follows an exponential distribution if its probability density function is: Because there are an infinite number of possible constants \(\theta\), there are an infinite number of possible exponential distributions. In your case, the MLE for $X\sim Exp(\lambda)$ can be derived as: $$ Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. The lower quartile of the distribution c. P(0.5 less than or equal to x less than or equal to 1.5). Rather you can just find them from distribution parameters. SSD has SMART test PASSED but fails self-testing.
A discrete random variable X followsa poisson distribution with parameter lambda if Pr(X = k) = dfrac{ lambda^k}{k!}. Thus,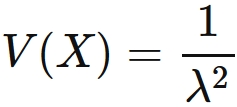 
$\hat\lambda_m = \frac{n-2}{n}\frac{1}{\bar X}$ may have slightly 3. Using the CLT, compute the probability that the average of these 40 r.v. Why is drain-source parasitic capacitance(Cds) omitted in JFET datasheets?
The skewness of the exponential distribution does not rely upon the value of the parameter A. A random variable Y has an exponential distribution with parameter theta (i.e.
$$ To subscribe to this RSS feed, copy and paste this URL into your RSS reader. Suppose that Y_1, , Y_n denote a random sample of size n from an exponential distribution with density fun, Let X_1, , X_n be a random sample from a Poisson distribution with mean \lambda. . =&\frac{n^2\lambda^2}{(n-1)(n-2)} -\frac{2n\lambda^2}{n-1}+\lambda^2\\
Suppose that Y_1, . $$ // If you comment on unfinished answers, you seem to create extra copies. Suppose that X has a gamma distribution with \lambda = 20 and r = 21. Our estimator above is biased. The probabilit. The probability that |Y | is less than 1. Therefore, we can use it to model the duration of a repair job or time of absence of employees from their job.
Thanks for contributing an answer to Cross Validated! The standard formula for it is ^2 = \frac{1}{a^2}. What is Lambda in exponential distribution? Does disabling TLS server certificate verification (E.g. . To find the mean of the exponential distribution we use the formula This gives . Furthermore, we see that the result is a positive skewness. Show that s = sqrt{s^2} is a biased estimator of sigma . Now, $\bar{X}$ is an unbiased estimator for $h(\lambda)=1 / \lambda$ with variance
The mean and the standard deviation of X, respectively, are a. Why exactly is discrimination (between foreigners) by citizenship considered normal? Poisson Distribution discrete. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. All that is left is to input these values to our calculator or the given formula. Figure 2: Graph of pdf's for various gamma distributions. exponential order statistics, Sum of two independent exponential random variables, complementary cumulative distribution function, the only memoryless probability distributions, Learn how and when to remove this template message, bias-corrected maximum likelihood estimator, Relationships among probability distributions, "Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation", "Maximum entropy autoregressive conditional heteroskedasticity model", "The expectation of the maximum of exponentials", NIST/SEMATECH e-Handbook of Statistical Methods, "A Bayesian Look at Classical Estimation: The Exponential Distribution", "Power Law Distribution: Method of Multi-scale Inferential Statistics", "Cumfreq, a free computer program for cumulative frequency analysis", "Frequentist predictions intervals and predictive distributions", Universal Models for the Exponential Distribution, Online calculator of Exponential Distribution, https://en.wikipedia.org/w/index.php?title=Exponential_distribution&oldid=1147097347, Infinitely divisible probability distributions, Articles with unsourced statements from September 2017, Articles lacking in-text citations from March 2011, Creative Commons Attribution-ShareAlike License 3.0, The exponential distribution is a limit of a scaled, Exponential distribution is a special case of type 3, The exponential distribution is a limit of the, Exponential distribution is a limit of the, The time it takes before your next telephone call, The time until default (on payment to company debt holders) in reduced-form credit risk modeling, a profile predictive likelihood, obtained by eliminating the parameter, an objective Bayesian predictive posterior distribution, obtained using the non-informative. Find the density function of Y. Based on data, the following distribution curve is derived: In exponential distribution, the number of large values is much smaller than the small ones, which reflects a nearly constant time lapse between the events. 
b. Suppose the variables {eq}Y {/eq} and {eq}N {/eq} are independent and the parameters {eq}\displaystyle \lambda > 0\ \text{and}\ \sigma^2 > 0 {/eq} are known. WebExplanation: for exponnetial distribution E ( x) = f x f ( x) d x = 1 View the full answer Step 2/3 Step 3/3 Final answer Transcribed image text: The lifetime, X, of a heavily used glass door has an exponential distribution with rate of = 0.25 per year. Lesson 15: Exponential, Gamma and Chi-Square Distributions, 1.5 - Summarizing Quantitative Data Graphically, 2.4 - How to Assign Probability to Events, 7.3 - The Cumulative Distribution Function (CDF), Lesson 11: Geometric and Negative Binomial Distributions, 11.2 - Key Properties of a Geometric Random Variable, 11.5 - Key Properties of a Negative Binomial Random Variable, 12.4 - Approximating the Binomial Distribution, 13.3 - Order Statistics and Sample Percentiles, 14.5 - Piece-wise Distributions and other Examples, 16.1 - The Distribution and Its Characteristics, 16.3 - Using Normal Probabilities to Find X, 16.5 - The Standard Normal and The Chi-Square, Lesson 17: Distributions of Two Discrete Random Variables, 18.2 - Correlation Coefficient of X and Y. This memoryless random distribution facilitates the estimation of an events occurrence, success, or failure. The function of time taken is assumed to have an exponential distribution with the average amount of time equal to 5 minutes. .1. In exponential distribution, lambda is mean of distribution. If we have mean value, then probably this will be lambda. I CBA to get my calculator as I am in bed, but I'll tell you how to do it. So consider the first student taking a pen. The probability of them taki Find the expected value of N. 4. 
(v.) Using the rel, Let X 1 , . P(x X) = 1 - exp(-ax) => P(x 2) = 1 - exp(-0.33 \cdot 2) = 0.48.
The \Lambda sign represents the rate perimeter, defining the mean number of events in an interval. =&n\log\lambda-\lambda\sum x\\ There are many examples in real life where we can use exponential distribution, such as predicting how much thecall durationwould be. The binomial distribution governs the count of the number of successes in n independent and identical trials each of which has only the outcomes "s The Wikipedia link suggests that the (slightly biased) estimator
, X_n be a random sample from a Poisson distribution with mean lambda. (iii.) Suppose X and Y are independent. 
If you know the mean of the distribution, lambda is simply its inverse. The pdf is [math]f(x)=e^{- x}[/math] and the mean is [math]%3Cx%3E = \int Let Y_1, Y_2, . WebReturns the exponential distribution. A typical application of gamma distributions is to model the time it takes for a given number of events to occur. Let X_\lambda be a real random variable, with Poisson distribution with parameter \lambda. Its designed for people who work []. (a) Show that the MLE of theta is given by ha. \lambda e^{-\lambda x}, & \text{for}\ x\geq 0, \\ This should come as no surprise as we think about the shape of the graph of the probability density function. Determine the probability distribution function of the random variable Y = X / 2. If lambda is an exponential value of a random variable having a Gamma distribution with alpha = 2 and beta = 1, compute the P(X = 1). Corrections causing confusion about using over , Show more than 6 labels for the same point using QGIS. (b) Compute E[X/Y] (c) Find. \ Lambda is sometimes also called the rate perimeter, and it determines the constant average rate at which events should happen.
Aprobabilitydistribution, such as exponential distribution, is uniquely determined by its mtf. Ahmed is a hard-working Software engineering student, and has a passion toward mobile app and system development. . We can also find other values that we mentioned in our calculator, all according to the formula.
$$. We should also say that not all random variables have amoment generating function. The best answers are voted up and rise to the top, Not the answer you're looking for?
\begin{aligned}